Graph theory to model Ticket to ride

This post contains a basic analysis of the mathematical model behind the board game Ticket to Ride by leveraging graph theory.

As you know, “Ticket to Ride” is a game where players aim at completing train routes in the most efficient way possible. The first version of the game is set in the United States of America in the late 19th century during the railroad expansion.

Modeling the game is understood as assessing the distribution of:

Number of tracks and associated colors
Track lenghts (i.e. number of wagons required to complete the track)
Shortest route between two stations¡

Analysis

To do this analysis, we have used following key libraries:

Pandas for data loading and processing
NetworkX for graph processing and above all, to find the shortest path between two stations (nodes).

First we will need to install some required libraries as well as import necessary modules

!pip install matplotlib networkx pandas

import matplotlib.pyplot as plt
import networkx as nx
import pandas as pd

The following cells contain some constants used in the notebook as well as the links to the CSVs that contain the Tracks and routes

TRACK_LENGTH_COLUMN = 'length'
FROM_COLUMN = 'from'
TO_COLUMN = 'to'

TRACKS_CSV_FILE = 'Ticket_to_ride - Tracks.csv'
TICKETS_CSV_FILE = 'Ticket_to_ride - Tickets.csv'

First let’s load the Track CSV, this will be used to visualize the track network as a mathetmatical graph (of nodes/stations and edges/tracks). The CSV contains the two stations for each track as well as their associated color and lenghts (number of wagons required to complete the track)

df = pd.read_csv(TRACKS_CSV_FILE)
df[TRACK_LENGTH_COLUMN] = pd.to_numeric(df[TRACK_LENGTH_COLUMN])
df.head()

	from	to	color	length
0	Washington	New York	black	2
1	Pittsburgh	Chicago	black	3
2	Raleigh	Nashville	black	3
3	Duluth	Winnipeg	black	4
4	Kansas City	Denver	black	4

With this DataFrame we can know useful information such as:

Number of total tracks
Number of wagons required for each color
Track distribution for each color

In addition, we can use the DataFrame to create the graph using the networkx library and make a visual representation of the track network

# Create a directed graph with weighted edges
graph = nx.from_pandas_edgelist(df, FROM_COLUMN, TO_COLUMN, edge_attr=TRACK_LENGTH_COLUMN, create_using=nx.Graph())

# Plot the graph
pos = nx.spring_layout(graph, weight=TRACK_LENGTH_COLUMN, seed=4)
nx.draw(graph, pos, with_labels=True, node_size=400, node_color='skyblue', font_size=9, font_color='black', font_weight='bold', edge_color='grey', linewidths=2)

# Add edge labels showing weights
edge_labels = nx.get_edge_attributes(graph, TRACK_LENGTH_COLUMN)
nx.draw_networkx_edge_labels(graph, pos, edge_labels=edge_labels)

# Display the plot
plt.show()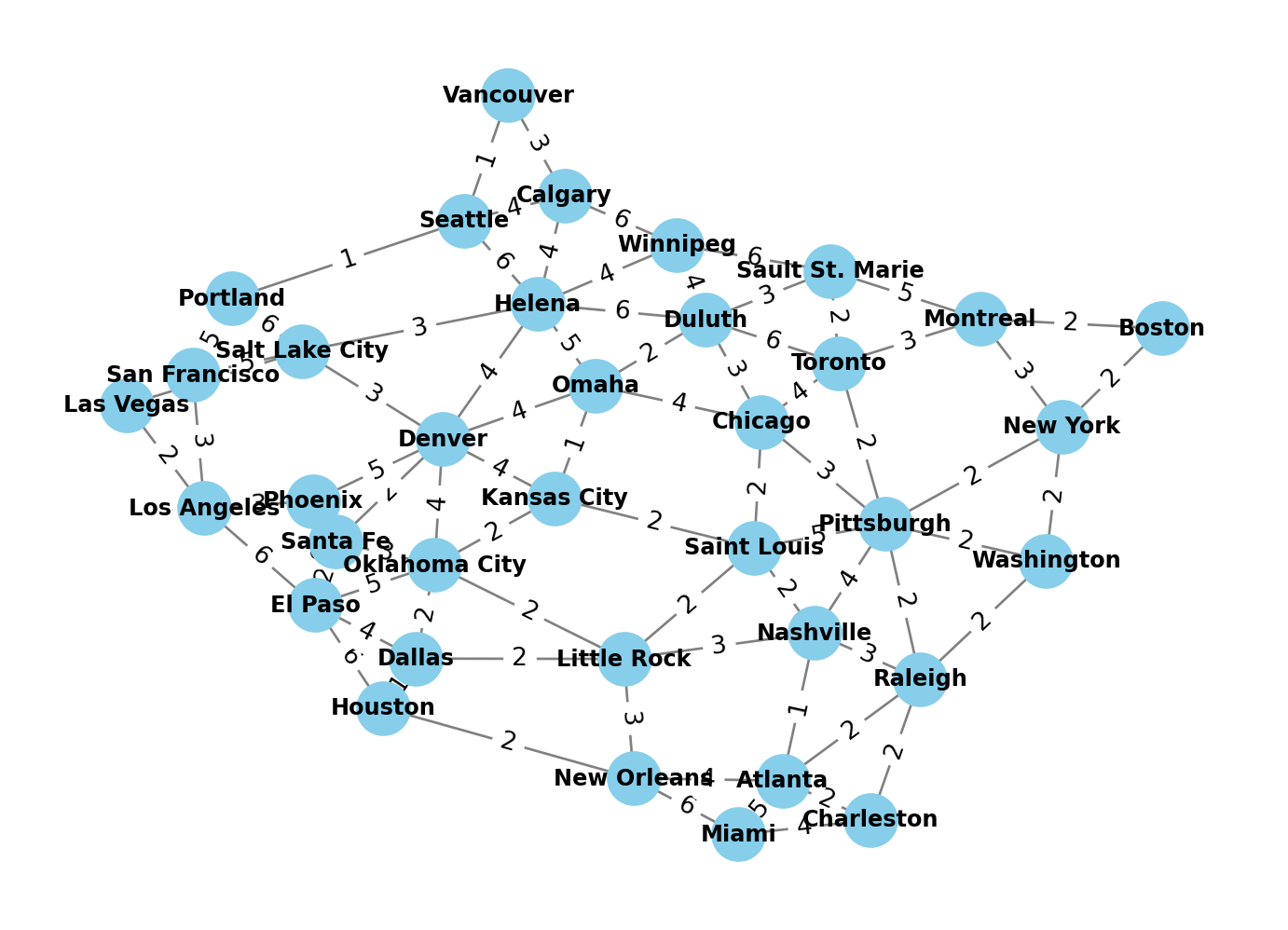

The advantage of modeling the track network as a graph is that we can use already existing libraries to compute the shortest path between two stations (both the passing stations as well as the total length), as in the following example

FROM = 'El Paso'
DESTINATION = 'Raleigh'

shortest_path = nx.shortest_path(graph, source=FROM, target=DESTINATION, weight=TRACK_LENGTH_COLUMN)
print(f'The shortest path goes through these stations: {" - ".join(shortest_path)}' )

shortest_path_length = nx.shortest_path_length(graph, source=FROM, target=DESTINATION, weight=TRACK_LENGTH_COLUMN)
print(f'The length for the shortes path is: {shortest_path_length}')

The shortest path goes through these stations: El Paso - Dallas - Little Rock - Nashville - Raleigh
The length for the shortes path is: 12

The shortest path goes through these stations: El Paso - Dallas - Little Rock - Nashville - Raleigh
The length for the shortes path is: 12

These methods (specially nx.shortest_path_length) are very relevant to reverse engineer the ticket cards (that give points if a player completes a route). Basically we need to know how the points awarded per card is related to the shortest path.

To do so, we will load the Ticket CSV into a DataFrame and compute the shortest path for each card:

# Load the Ticket CSV
df_tickets = pd.read_csv(TICKETS_CSV_FILE)

# Create a new column in the dataframe with the shortest path length for each route (i.e. ticket card)
df_tickets[TRACK_LENGTH_COLUMN] = df_tickets.apply(lambda r: nx.shortest_path_length(graph, source=r[FROM_COLUMN], target=r[TO_COLUMN], weight=TRACK_LENGTH_COLUMN), axis=1)

df_tickets.head()

	from	to	points	length
0	Los Angeles	New York	21	20
1	Winnipeg	Little Rock	11	11
2	Vancouver	Santa Fe	13	13
3	Montreal	Atlanta	9	9
4	Toronto	Miami	10	10

At this point we can realise that the points awarded per route are in fact equivalent (at least on the most cases) with the lenghts (i.e. total number of wagons required to complete the route), which makes sense.

plt.plot(df_tickets[TRACK_LENGTH_COLUMN], df_tickets['points'], 'o')
plt.xlabel('Shortest route length [number of wagons]')
plt.ylabel('Ticket card points')
plt.title('Relationship between Ticket card points and\nShortest route length')
plt.show()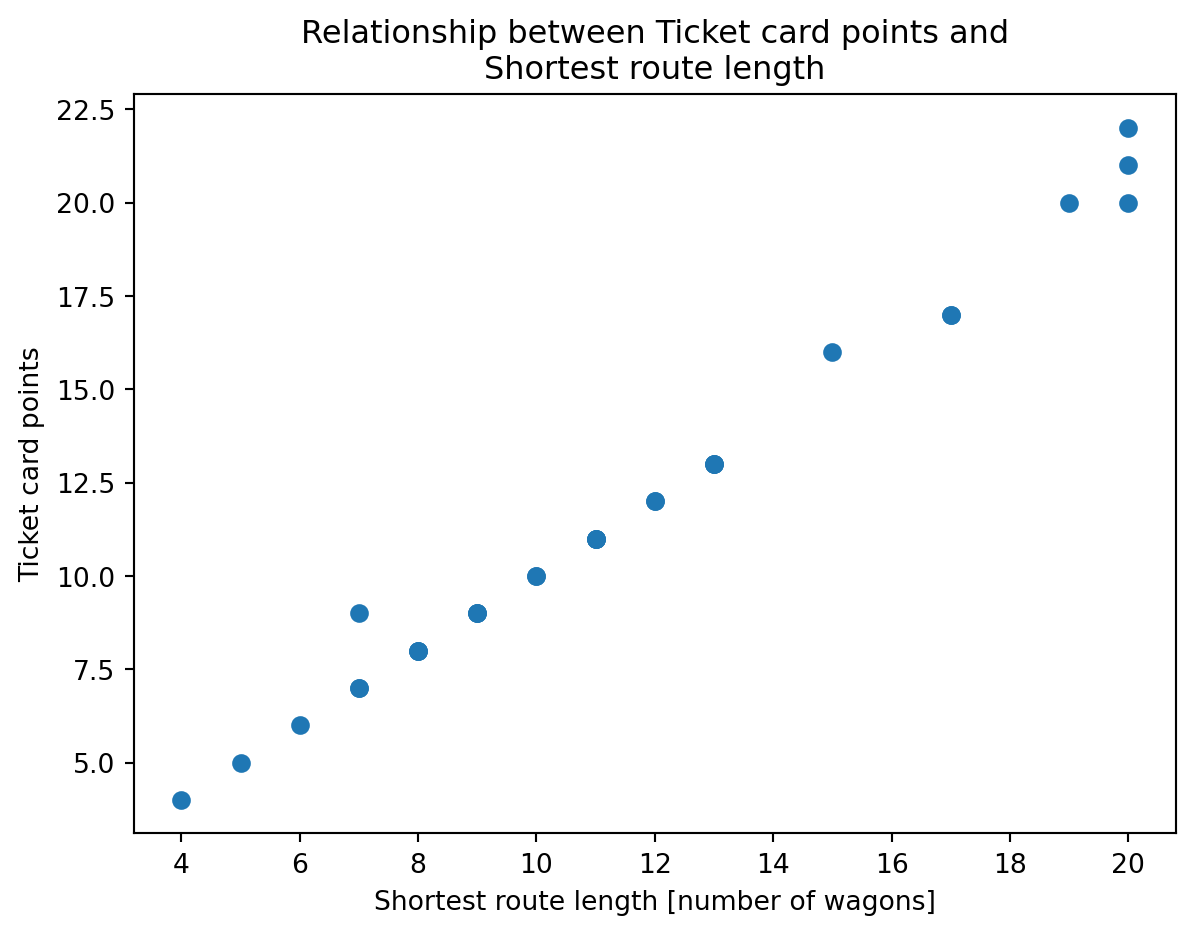

Key takeaways

From the analysis, the following takeaways are relevant in case you need to make your own customization of Ticket to ride:

There are 36 stations
There are a total of 100 tracks (double tracks are considered independent tracks)
Each color (except grey) needs a total of 27 wagons to complete their tracks
Each color (except grey) has a total number of 7 tracks, and their distribution is: 6-5-4-4-3-3-2, except for green and white, for which their distribution is: 6-5-5-4-3-2-2.
To the largest possible extent, the colors are homogeneously distributed on the territory (which makes sense in order to balance the game).
There are 30 ticket cards
The points for each ticket card represent the shortest path length (i.e. minimum number of wagons required to complete the card), with some small exceptions.